Introducción¶
Se denomina ruido a toda señal no deseada que se mezcla con la señal útil que se quiere recibir. El ruido se debe a múltiples causas como al ruido térmico de los resistores, a las interferencias de señales externas, etc. No es posible eliminar totalmente el ruido, ya que los componentes electrónicos no son perfectos y por la temperatura a la que operen. Sin embargo, es posible minimizar su efecto.
La distorsión que produce el ruido en una determinada comunicación depende de su potencia, de su distribución espectral respecto al ancho de banda de la señal y de la propia naturaleza de información que transporta. Como el ruido es un proceso aleatorio, puede ser caracterizado por variables como varianza, distribución y destino espectral.
La distribución espectral del ruido puede variar por la frecuencia, y su densidad de potencial es medida en $ \left[ \frac{W}{Hz}\right]`$. Como la potencia de un elemento resistivo es proporcional a la raíz cuadrada del voltaje alrededor del elemento, la unidad de la densidad de voltaje del ruido podría escribirse como :math:left[ frac{V}{sqrt{Hz}}right]`. Se define como ruido blanco aquel que su densidad espectral de ruido en frecuencia es constante. Para medir la influencia del ruido sobre la señal se utiliza la relación señal/ruido, que generalmente se emplea en \(dB\).
Tipos de ruido¶
Ruidos correlacionados¶
El ruido correlacionado es producido por amplificaciones no lineales e incluye armónicos y distorsión de intermodulación, que son dos formas de distorsión no lineal.
Distorsión armónica: Se define como la producción de armónicos de una señal originados por una mezcla no lineal. Los armónicos son múltiplos enteros de la señal original de entrada, la señal original es la primer armónica y se conoce como la frecuencia fundamental.
Distorsión de intermodulación: se refiere a la generación indeseable de productos cruzados que son la suma o restas de frecuencias.
Ruidos no correlacionados¶
Ruido de disparo¶
El ruido de disparo en dispositivos electrónicos es el resultado de fluctuaciones estadísticas aleatorias inevitables de la corriente eléctrica cuando los portadores de carga (como los electrones) atraviesan un espacio. Si los electrones fluyen a través de una barrera, entonces tienen tiempos discretos de llegada. Esas llegadas discretas exhiben ruido de disparo. Típicamente, se usa la barrera en un diodo. [3] El ruido de disparo es similar al ruido creado por la lluvia que cae sobre un techo de hojalata. El flujo de lluvia puede ser relativamente constante, pero las gotas de lluvia individuales llegan discretamente.
El valor de la raíz cuadrada media de la corriente de ruido de disparo está dada por la fórmula de Schottky,
donde \(I\) es la corriente continua, \(q\) es la carga de un electrón y \(\Delta B\) es el ancho de banda en hertz. La fórmula de Schottky supone llegadas independientes.
Los tubos de vacío presentan ruido de disparo porque los electrones abandonan aleatoriamente el cátodo y llegan al ánodo (placa). Es posible que un tubo no muestre el efecto de ruido de disparo completo: la presencia de una carga espacial tiende a suavizar los tiempos de llegada (y así reducir la aleatoriedad de la corriente).
Los conductores y las resistencias normalmente no muestran ruido de disparo porque los electrones se encuentran en equilibrio térmico y se mueven difusamente dentro del material; los electrones no tienen tiempos de llegada discretos. El ruido de disparo se ha demostrado en resistencias mesoscópicas cuando el tamaño del elemento resistivo se vuelve más corto que la longitud de dispersión del electrón-fonón.
Debe distinguirse el ruido de disparo de las fluctuaciones de corriente en equilibrio, las cuales se producen sin aplicar ningún voltaje y sin necesidad de que exista ningún flujo promedio de corriente. Estas fluctuaciones de la corriente de equilibrio se conocen como ruido de Johnson-Nyquist.
El ruido de disparo se puede modelar como un proceso de Poisson y los portadores de carga que forman la corriente siguen una distribución de Poisson. El ruido de disparo está yuxtapuesto a cualquier ruido presente, y se puede demostrar que es aditivo respecto al ruido térmico y a él mismo.
Ruido Flicker¶
Ruido Flicker o ruido \(1/f\) presenta un densidad espectral que crece, por debajo de kilo-hertz, al disminuir la frecuencia. También es llamado ruido en exceso o ruido de semiconductor, habiéndose atribuido diferentes orígenes, entre ellos los procesos aleatorios de generación-recombinación térmica de pares electrón-hueco, dicho en otras palabras es una señal con una frecuencia de espectro que cae, proporcional a la magnitud de la señal, es más importante a bajas frecuencias y para anchos de banda pequeños $1/f $es aproximadamente constante.
Ruido Térmico¶
El ruido térmico (a veces térmico, Johnson o Nyquist) es inevitable y se genera por el movimiento térmico aleatorio de los portadores de carga (generalmente electrones), dentro de un conductor eléctrico, que ocurre independientemente de cualquier voltaje aplicado. Este ruido sera desarrollado en la siguiente sección.
Ruido Térmico en Resistores.¶
También conocido como ruido Johnson-Nyquist), es el ruido generado por el equilibrio de las fluctuaciones de la corriente eléctrica dentro de un conductor eléctrico, el cual tiene lugar bajo cualquier voltaje, debido al movimiento térmico aleatorio de los electrones.
El ruido térmico es aproximadamente blanco, lo que significa que su densidad espectral de potencia es casi plana (hasta frecuencias cercanas a los THz). Además, la amplitud de la señal sigue una distribución gaussiana.
Fuente de tensión de ruido blanco¶
El ruido térmico es diferente del ruido de disparo, que tiene lugar cuando el número finito de electrones es suficientemente pequeño para dar lugar a la aparición de fluctuaciones estadísticas apreciables en una medición. La definición de ruido de Johnson-Nyquist aplica a cualquier tipo de medio conductor. Puede modelarse como una fuente de tensión que representa el ruido de una resistencia eléctrica no ideal en serie con una resistencia eléctrica libre de ruido. Los modelos equivalentes de un resistor se muestran en la siguiente figura.
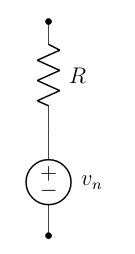
La densidad espectral de potencia de ruido en un resistor esta dada por:
Donde $ k_B $ es la constante de Boltzmann, \(T\) es la temperatura a la que se halla el resistor en grados kelvin [\(K\)], y $ R $ su valor en Ohmios [\(\Omega\)].
La constante de Boltzman toma un valor aproximado de:
Si queremos encontrar la potencia de ruido generada en un ancho de banda B, solo debemos multiplicar la densidad espectral de potencia por el mismo. Por lo tanto, el valor cuadrático medio de la tensión en el resistor esta dado por por:
Donde
\(h\) = Constante de Planck
\(k_B\) = Constante de Boltzmann
\(T\) = temperatura absoluta en Kelvin
\(B\) = ancho de banda en Hz
\(f\) = frecuencia central de la banda en Hz
\(R\) = resistencia
Es posible simplificar esta ecuación, donde es puede usarse hasta \(100\,GHz\) y temperaturas mayores a los \(100\,K\):
Fuente de corriente de ruido blanco¶
Utilizando el teorema de Norton es posible obtener el dual de la expresión anterior para la corriente de ruido en el resistor.
Donde G es la inversa de la resistencia R, su conductancia.
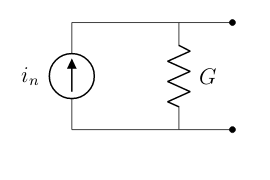
Observar que sucedería si fuera posible medir el valor de tensión con un instrumento de ancho de banda infinito, el valor de tensión medido seria infinito. Esto no es posible debido a que como mencionamos anteriormente, la aproximación de densidad espectral de potencia plana solo es valida hasta frecuencias cercanas a los THz, para frecuencias más altas, se debe tener en cuenta que la densidad espectral toma la siguiente forma.
La expresión anterior es similar a la expresión de la irradiancia espectral de un cuerpo negro y es así debido a la estrecha relación entre la agitación térmica de los electrones dentro de un solido y la radiación electromagnética que emite.
Para frecuencias bajas \(hf << h f\) por lo tanto, la densidad espectral se reduce a la expresión \(N_{Res} = 4 k_B T R\).
Simulación de la densidad de ruido espectral.¶
Cada resistencia ofrece en sus terminales una Potencia de ruido disponible de:
La densidad de potencia de ruido es la potencia que se puede medir en cada Hz del ancho de banda. El total potencia disponible se obtiene si se multiplica esta densidad por el ancho de banda válido (o por integración sobre el ancho de banda si la densidad de potencia de ruido varía con el ancho de banda).
Pero frecuentemente se prefiere manejar voltaje en lugar de la potencia, porque es más fácil medir voltajes a diferentes frecuencias que la potencia. Entonces se usa la ecuación de potencia para operar con los dos valores:
Cuando se calcula la raíz cuadrada de la Densidad de potencia de ruido, obtendrá una expresión para la «Densidad de voltaje de ruido espectral», dada en [V/\(\sqrt[]{Hz}\)]. Si se multiplica este valor por \(\sqrt[]{Hz}\), se obtiene el voltaje total de ruido.
Ejemplo 1¶
Para una resistencia de \(1 K\Omega\) a $ 300 K$ el valor medio cuadrático de ruido de la tensión sobre el resistor es:
Valor de tensión sobre el resistor: \(4.07e-09 V/\sqrt{Hz}\)
Simulación con LTspice, midiendo la densidad de tensión de ruido¶
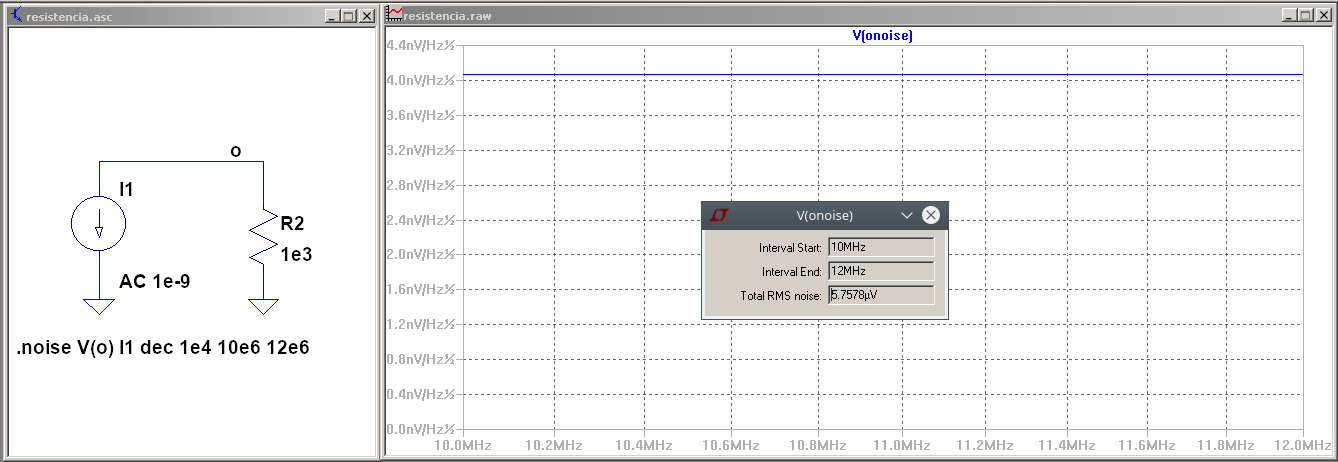
Cifra de ruido y Factor de ruido:¶
La cifra de ruido (NF) y el factor de ruido (F) son medidas de degradación de la relación señal/ruido (SNR) causada por componentes en una cadena de señal.
El factor de ruido es, por lo tanto, la relación entre el ruido de salida real y el que se mantendría si el propio dispositivo no introdujera ruido, o la relación de la entrada SNR a la salida SNR.
La cifra de ruido es simplemente el factor de ruido (F) expresado en decibelios (dB).
Operando el factor de ruido, es posible obtener otras formas de calcularlo.
La potencia de ruido a la salida \(N_o\) puede ser expresar como \(N_o = G N_o + N_e\), entonces:
\(N_e\) es la potencia en exceso a la salida y se puede calcular como:
Para un circuito paralelo (modelo admitancia), la potencia adicional puede ser suministrada por una fuente de corriente.
donde \(i_i = \sqrt{4\cdot k_b \cdot T \cdot B \cdot \frac{1}{R} }\)
Si la fuente \(N_e\) esta en la entrada, \(N_e = G \cdot N_ei\)
La potencia $N_{ei} $ corresponde a una potencia de ruido excedente que se presenta en la entrada y se puede calcular como:
Para un circuito paralelo (modelo admitancia), la potencia adicional puede ser suministrada por una fuente de corriente.
donde \(i_i = \sqrt{4\cdot k_b \cdot T \cdot B \cdot \frac{1}{R} }\)
Fuentes de ruido en LTspice¶
Un caso en el que dichas fuentes de ruido pueden ser útiles es cuando se realizan modelos de simulación de amplificadores donde se conoce el voltaje de entrada referido y los ruidos de corriente a partir de la hoja de datos. La única fuente de ruido simple (que afecta a las simulaciones de ruido) en LTspice es una resistencia simple. Existen otras fuentes de ruido en los modelos de dispositivos semiconductores, pero esos modelos son más complejos. Una resistencia ideal tiene un ruido de voltaje descrito por:
donde \(k_B\) es la constante de Botzmann (\(1.381\times 10^{-23} J/K\)), \(T\) es la temperatura en Kelvin (\(300\, K\) por defecto en LTspice), \(B\) es el ancho de banda en [Hz] y \(R\) es La resistencia en [\(\Omega\)]. En las hojas de datos de los transistores o amplificadores generalmente especifica el ruido de voltaje blanco en unidades de \([\frac{nV}{\sqrt{Hz}}]\) y el ruido de corriente en \([\frac{pA}{\sqrt{Hz}}]\) (a veces \([\frac{fA}{\sqrt{Hz}}]\)).
Para crear una fuente de ruido de voltaje blanco, podemos conectar los terminales de entrada de una fuente de voltaje dependiente de voltaje a una resistencia y usar un factor de escala adecuado. La fuente dependiente aísla la resistencia de cualquier circuito que esté conectado a ella y preserva la amplitud de ruido de voltaje independientemente de la carga. Dado que las fuentes de ruido generalmente se especifican en nV/√Hz, es conveniente poder ingresar ese número directamente como parte del modelo. Una forma simple de hacerlo es seleccionando una resistencia que produce una densidad de ruido de 1 \(\frac{nV}{\sqrt{Hz}}\) e ingrese la amplitud de ruido de la hoja de datos como la ganancia de voltaje de la fuente dependiente. Resolviendo la ecuación anterior para \(v_n = 1 nV\) cuando \(T = 300 K\) y \(B = 1 Hz\) da \(R = 60.342\).
El esquema de la especificación LTspice resultante para una fuente de ruido de voltaje de 2 \(\frac{nV}{\sqrt{Hz}}\) es así:
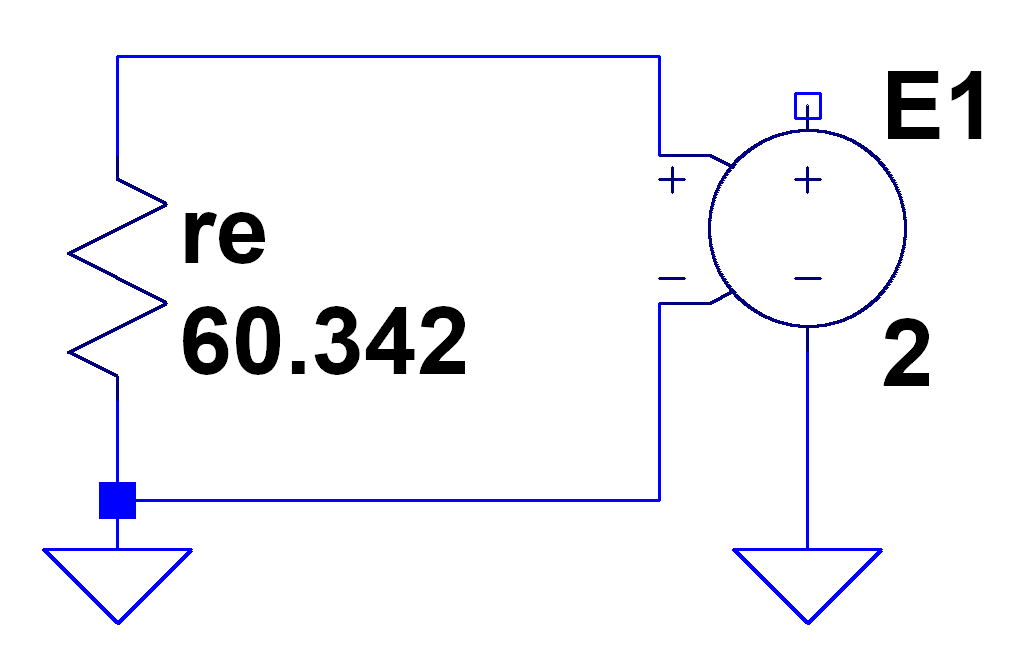
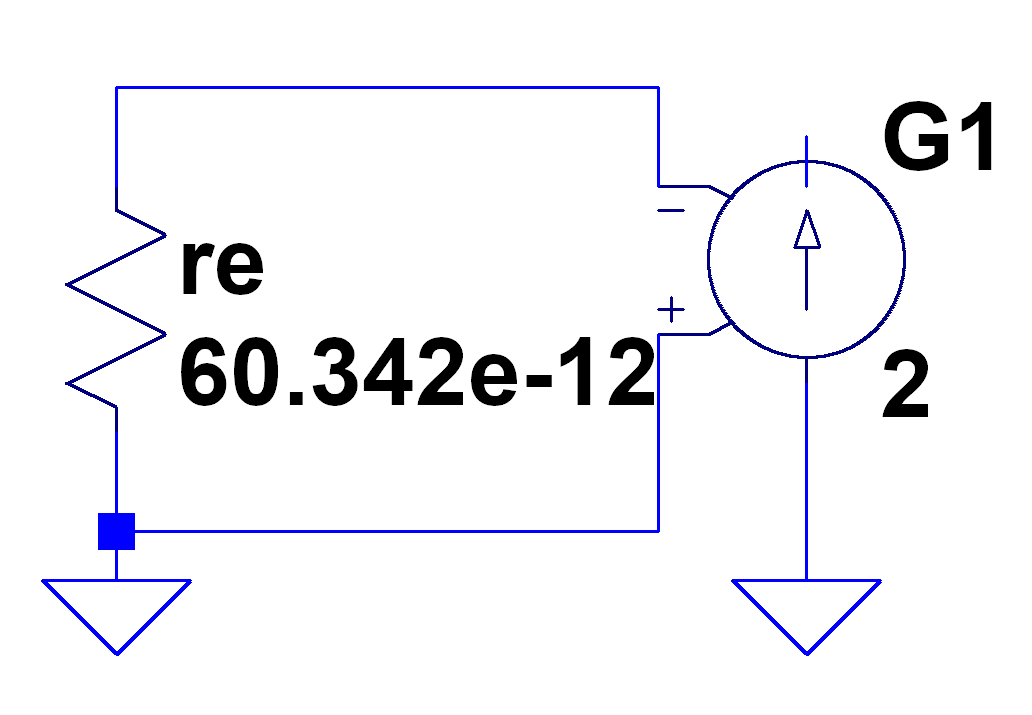
De manera similar, para crear una fuente de ruido de corriente blanca, podemos usar una fuente de corriente dependiente de voltaje ( Fuente de G). Para establecer el factor de transconductancia de la fuente a la densidad de ruido en \([\frac{pA}{\sqrt{Hz}}]\), es necesaria una resistencia con una densidad de ruido de 1 \(\frac{pA}{\sqrt{Hz}}\), lo que significa que la resistencia tendrá un valor de $60.342e-6 $.
Una fuente de ruido de corriente con una densidad de ruido de 2 \(\frac{pA}{\sqrt{Hz}}\) se puede modelar así:
Ejemplo de Factor de ruido en amplificadores¶
Suponiendo un transistor con cifra de ruido de \(3 dB\), calcular la corriente en excedo de la fuente del transistor.
Parametros del transistor:
,
,
.
Medición de la potencia de ruido en la entrada sin ruido en exceso¶
Se mide la potencia de ruido en la entrada. Esta potencia de ruido es suminstrada por las resistencias del nodo de entrada (generador y transistor).
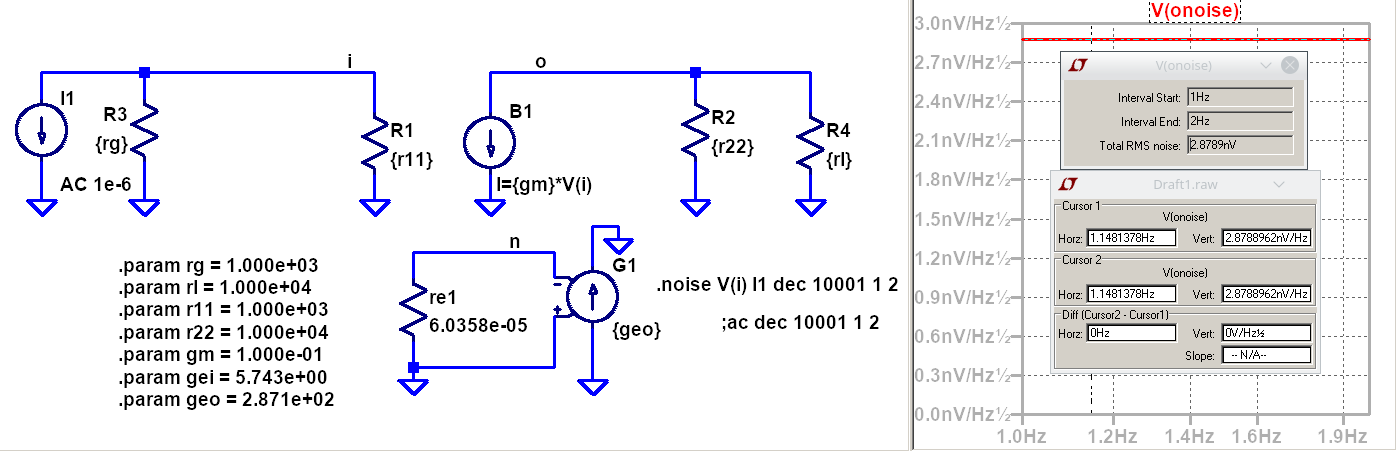
De la medición, la tensión espectral de ruido en la entrada es:
\(V_n = \sqrt{4\cdot k_b \cdot T \cdot r_{ti} } = 2.87 \frac{n V}{\sqrt{Hz}}\)
El valor de tensión rms ($ 1 Hz$ de ancho de banda):
\(V_{rms} = 2.87 \frac{n V}{\sqrt{Hz}} \cdot 1 Hz = 2.87 n V\)
La potencia de ruido en la entrada del transistor:
\(N_{i} = \frac{ (V_{rms})^2}{r_{11}} = \frac{ (2.87 n V)^2}{1K\Omega} = 8.28\times 10^{-21} W\)
Medición de la potencia de ruido en la salida sin ruido en exceso¶
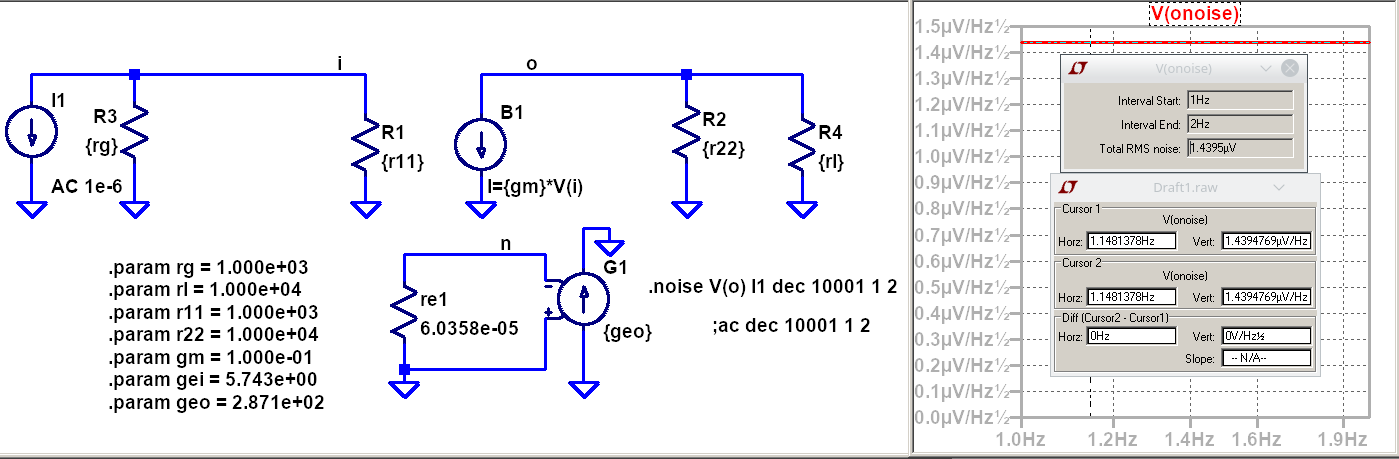
De la medición, la tensión espectral de ruido en la entrada es:
\(V_n = \sqrt{4\cdot k_b \cdot T \cdot r_{ti} } = 1.44 \frac{\mu V}{\sqrt{Hz}}\)
El valor de tensión rms ($ 1 Hz$ de ancho de banda):
\(V_{rms} = 1.44 \frac{\mu V}{\sqrt{Hz}} \cdot 1 HZ = 1.44 \mu V\)
La potencia de ruido en la resistencia de salida \(r_l\) :
\(N_{o} = \frac{ (V_{rms})^2}{r_{l}} = \frac{ (1.44 \mu V)^2}{10K\Omega} = 2.07\times 10^{-16} W\)
Ganancia de potencia¶
\(G = \frac{N_o}{N_i} = \frac{2.07\times 10^{-16}}{8.23\times 10^{-21}} = 25.1 \times 10^{3}\)
Analiticamente la ganancia de potencia \(G\) se puede calcular como:
\(G = |Av|^2 \cdot \frac{rl}{r11} = (gm \cdot r_{to})^2 \cdot \frac{rl}{r11} = 25 \times 10^{3}\)
Medición del Factor de ruido con ruido en exceso en la entrada¶
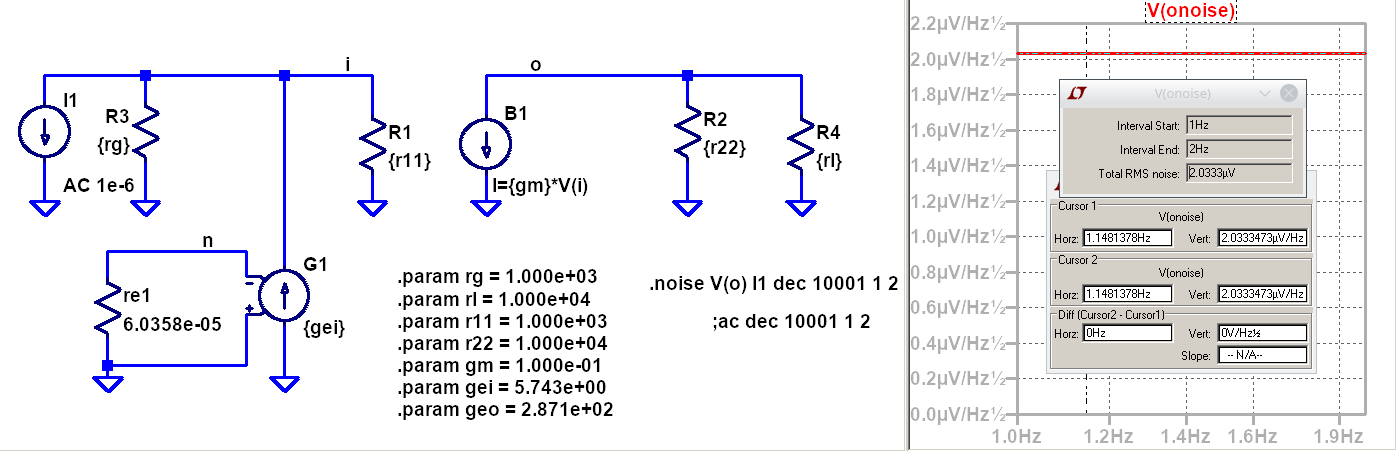
De la medición, la tensión espectral de ruido en la salida es:
\(V_n = \sqrt{4\cdot k_b \cdot T \cdot r_{ti} } = 2.03 \frac{\mu V}{\sqrt{Hz}}\)
El valor de tensión rms ($ 1 Hz$ de ancho de banda):
\(V_{rms} = 2.03 \frac{\mu V}{\sqrt{Hz}} \cdot 1 HZ = 2.03 \mu V\)
La potencia de ruido en la resistencia de salida \(r_l\) :
\(N_{o} = \frac{ (V_{rms})^2}{r_{l}} = \frac{ (2.03 \mu V)^2}{10K\Omega} = 4.12\times 10^{-16} W\)
El Factor de poptencia:
\(F = \frac{N_{o}}{G \cdot N_{i}} = \frac{4.12\times 10^{-16} W}{ 25\times 10^{3} \cdot 8.28\times 10^{-21} W} = 2\)
Medición del Factor de ruido con ruido en exceso en la salida¶
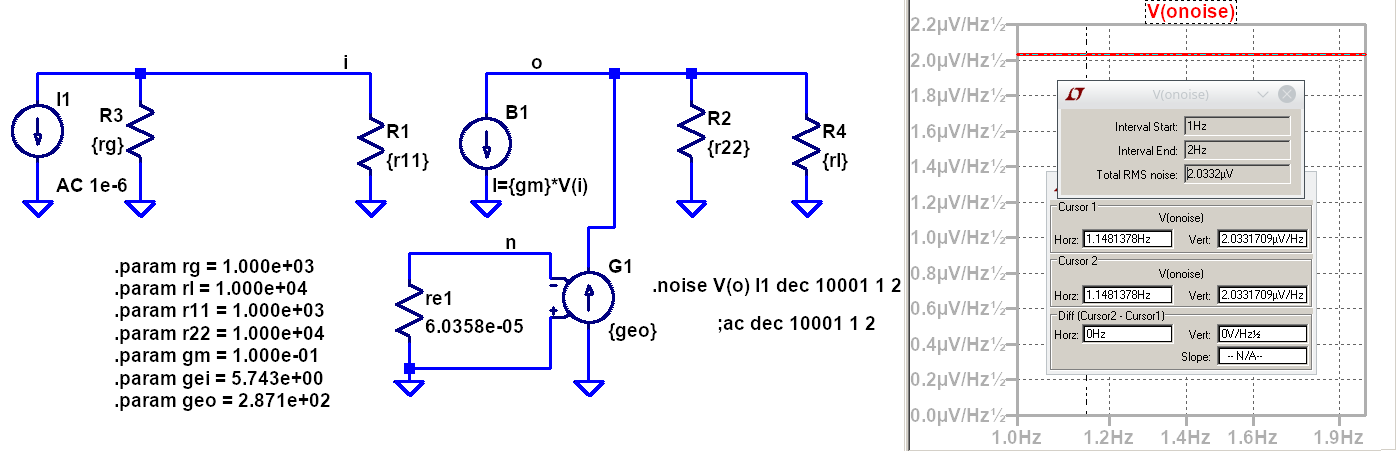
De la medición, la tensión espectral de ruido en la salida es:
\(V_n = \sqrt{4\cdot k_b \cdot T \cdot r_{ti} } = 2.03 \frac{\mu V}{\sqrt{Hz}}\)
El valor de tensión rms ($ 1 Hz$ de ancho de banda):
\(V_{rms} = 2.03 \frac{\mu V}{\sqrt{Hz}} \cdot 1 HZ = 2.03 \mu V\)
La potencia de ruido en la resistencia de salida \(r_l\) :
\(N_{o} = \frac{ (V_{rms})^2}{r_{l}} = \frac{ (2.03 \mu V)^2}{10K\Omega} = 4.12\times 10^{-16} W\)
\(F = \frac{N_{o}}{G \cdot N_{i}} = \frac{4.12\times 10^{-16} W}{ 25\times 10^{3} \cdot 8.28\times 10^{-21} W} = 2\)
Nota: en estos calculos se despreciaron los ruidos aportados por las resistencias en la salida.¶
Factor de ruido en dispositivos conectados en cascada.¶
La fórmula de Friis se utiliza para calcular el factor de ruido total de una cascada de etapas, cada una con su propio factor de ruido y ganancia de potencia (suponiendo que las impedancias se combinan en cada etapa).
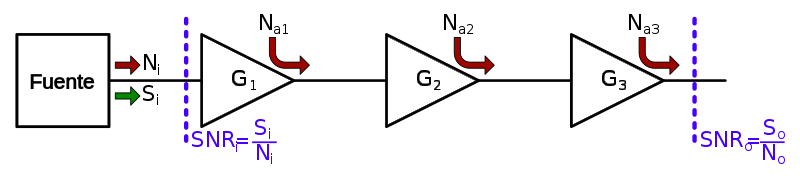
El factor de ruido total se puede utilizar para calcular la cifra de ruido total.
El factor de ruido total se da como
Suponiendo el sistema que se muestra en la figura, la potencia de señal a la salida se calcula como (suponiendo que el calculo de potencia tiene en cuenta la impedancia de entrada y de salida de las distintas etapas del sistema):
La potencia de ruido N_o en este caso sera:
El factor de ruido entonces:
A temperatura ambiente, el factor de ruido de una red con pérdidas es igual a su pérdida de potencia.
La potencia de ruido en la entrada del atenuador debido a una fuente perfectamente adaptada a la temperatura (\(T\)) viene dada por
La densidad espectral de potencia de ruido de entrada es
Cuando una señal ruidosa pasa a través del atenuador, la potencia de ruido se atenúa de la misma manera que la potencia de la señal (\(G = \frac{1}{L}\)). Entonces, la densidad espectral de potencia del ruido en la salida es
donde \(L = 10^{L_{dB}/10}\)
Solo sale una parte del ruido, y el resto se disipa en el atenuador. Bajo el supuesto de que el atenuador está en equilibrio térmico, no sale calor por el atenuador debido al gradiente de temperatura.
El calor disipado en el atenuador es equivalente al exceso de potencia de ruido (N_e) en el atenuador.
Factor de ruido del atenuador,
Ancho de banda equivalente¶
Hasta el momento el analisis realizado permite el calculo de la densidad espectral de ruido. Para conocer la potenica de ruido es necesario conocer el ancho de banda de los circuitos.
A continuación se analiza el ancho de banda de circuitos con impedacias complejas y luego, circuitos sintonizados.
Impedancias complejas¶
Nyquist determinó que la densidad espectral de ruido generado en una impedancia solo depende del valor resistivo de la impedancia (Parte real). El valor de tensión cuadrático medio en bornes de la impedancia se calcula integrando la densidad espectral sobre el ancho de banda de interés. El cálculo de la tensión de ruido tiene la siguiente expresión.
La expresión anterior equivale tener infinitas resistencias de valor \(R(f)\) que solo aportan ruido en un diferencial tensión cuadrática media \(4 k_B T R(f) df\) centrado en \(f\).
Para fijar conocimientos, consideremos un resistor en paralelo con un capacitor.
El valor de impedancia en bornes se calcula:
Donde
Por lo tanto, para conocer el valor cuadrático medio de la tensión de ruido a la salida debemos resolver la siguiente integral
Observar que la constante que multiplica a la integral tiene unidades de \(V^2/Hz\), por lo tanto, la integral debe tener unidades de \(Hz\). Más adelante veremos que esta integral determina el ancho de banda de ruido equivalente y esta dado pros la respuesta en frecuencia del circuito. Para resolver la siguiente integral, debemos conocer el ancho de banda sobre el que queremos medir el ruido, supongamos que poseemos un instrumento de ancho de banda infinito y queremos verificar el nivel de ruido,la integral que debemos resolver es:
Recurriendo a una tabla de integrales entonces:
Sabiendo que para un filtro RC, la frecuencia de corte se halla en \(f_{-3db}=\frac{1}{2 \pi R C}\). La tensión cuadrática media de ruido toma la expresión:
Donde el término entre paréntesis es el denominado ancho de banda equivalente de ruido.
[5]:
# Ejemplo de calculo de potencia de ruido
# RC en paralelo
## Calculo con Jupyter
kb = constants.value('Boltzmann constant')
T = 300 # K
R = 1e3 # ohm
C = 1e-9 # F
# Potencia de ruido
Prms = (kb*T/C)/R # [V/sqrt(Hz)]
print('Potencia de ruido sobre el resistor: {:1.2e} W'.format(((Prms))))
Vrms = (Prms*R)**(1/2)
print('Valor cuadratico medio de la tensión sobre el resistor: {:1.2e} V'.format(Vrms) )
Potencia de ruido sobre el resistor: 4.14e-15 W
Valor cuadratico medio de la tensión sobre el resistor: 2.04e-06 V
Medición con LTspice¶
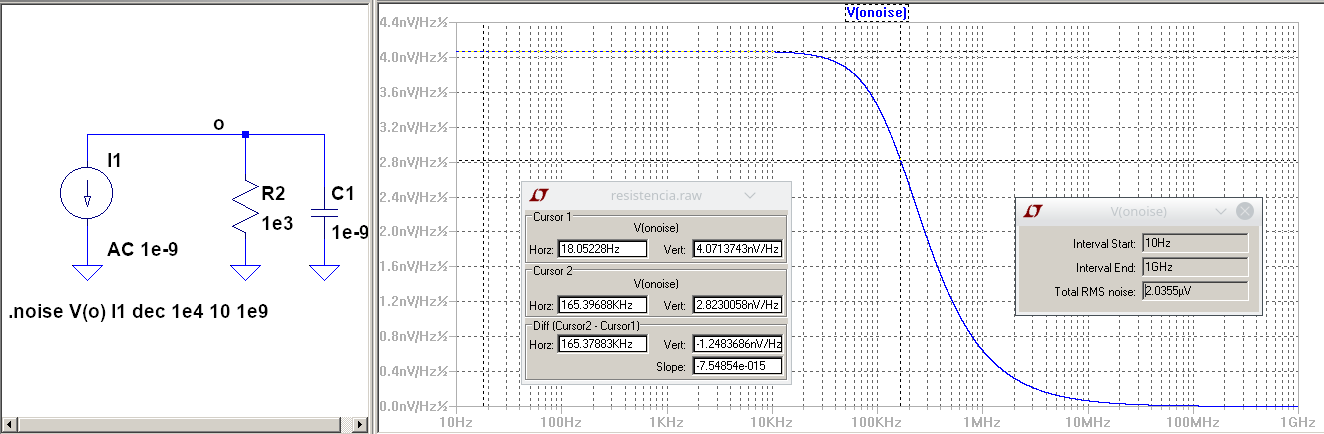
Valor cuadratico medio de la tensión sobre el resistor: \(2.04e-06 V\)
Potencia de ruido sobre el resistor:
Ancho de banda equivalente en circuitos sintonizados¶
Tanto el ruido térmico como el de disparo poseen densidades espectrales planas. Se define como ancho de banda equivalente de ruido de un sistema, al ancho de banda que debería tener un dispositivo ideal para producir en la salida la misma potencia de ruido. Esto re representa gráficamente en la siguiente imagen.
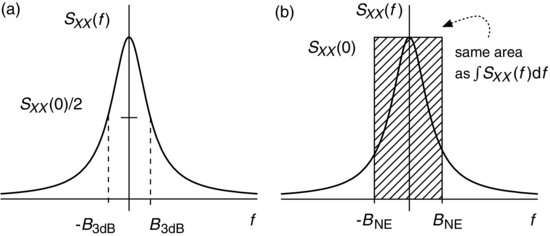
La potencia de ruido a la salida del dispositivo puede calcularse integrando la densidad espectral de potencia de ruido a la salida \(N_{noise}*|H(f)|^2\) para todas las frecuencias, donde \(|H(f)|^2\) es la ganancia de potencia en función de la frecuencia del dispositivo (puede ser un amplificador, un filtro o un mezclador). Esta potencia tiene que coincidir con la potencia a la salida de un filtro ideal de ancho de banda \(B_{eq}\) y ganancia igual a la ganancia en frecuencia central \(f_{c}\). Esto se expresa matemáticamente de esta forma:
\(P_{out}=\int_{-\infty}^{\infty} N_{0} \cdot |H(f)|^2 df= N_{0} \cdot |H(f_{c})|^2\int_{-B_{eq}/2}^{B_{eq}/2} df\)
Donde \(N_{noise}\) es la densidad espectral de ruido y una constante. Resolviendo la integral en el termino derecho se obtiene:
\(N_{0} \int_{-\infty}^{\infty} |H(f)|^2 df= N_{0} \cdot |H(f_{c})|^2 B_{eq}\)
Esto demuestra que el ancho de banda se calcula de la siguiente forma:
\(B_{eq}=\frac{\int_{-\infty}^{\infty} |H(f)|^2 df}{|H(f_{c})|^2}=\int_{-\infty}^{\infty} \frac{|H(f)|^2}{|H(f_{c})|^2} df =\int_{-\infty}^{\infty} \bar{|H(f)|^2} df\)
Para demostrar la aplicación de este concepto,calculemos el ancho e banda equivalente de ruido de un amplificador sintonizado. El mismo tiene la siguiente respuesta en frecuencia normalizada:
Donde: \(\chi^2=\frac{2 Q}{f_{c}} \cdot (f-f_{c})\), entonces \(df= \frac{f_{c}}{2Q}d\chi\). El ancho de banda equivalente se calcula de esta forma
Este resultado es el mismo que el del filtro RC calculado anteriormente. El ancho de banda equivalente es el ancho de banda de 3dB por \(\pi/2\)
Donde: \(\chi^2=\frac{2 Q}{f_{c}} \cdot (f-f_{c})\), entonces \(df= \frac{f_{c}}{2Q}d\chi\). El ancho de banda equivalente se calcula de esta forma
Este resultado es el mismo que el del filtro RC calculado anteriormente. El ancho de banda equivalente es el ancho de banda de 3dB por \(\pi/2\)
En el caso de un amplificador doble sintonizado, la transferencia normalizada es:
Ejemplo Simple Sintonizado empleando transistor con cifra de ruido $ NF = 2 dB $.¶
Calcular el ancho de banda equivalente de un amplificador simple sintonizado. Calcular para máxima transferencia de energía. Suponer que el aporte de la fuente de ruido en exceso se encuentra en la entrada.
Datos: \(f_o = 100 MHz\)
\(Q_c = 40\)
\(Q_o = inf\)
Transistor: \(y11= 1.0 mS\), \(y12= 0.0 mS\), \(y21= 30.0 mS\), \(y22= 0.1 mS\).
[6]:
## Ejemplo con calculo en Python
# simple sintonizado de 100MHz
# Frecuencia de operación
fo = 100e6
wo= 2*np.pi*fo
kb = constants.value('Boltzmann constant')
# Temperatura en Kelvin
T = 300
# Parametros del transistor 100 MHz
y11 = 1.0e-3
y12 = 0.0
y21 = 30.0e-3
y22 = 0.1e-3
# Cifra de ruido del transistor
NF = 2 # dB
F = 10**(NF/10) # Factor de ruido del transistor
Q1 = 40 # Q cargado del sintonizado
Qo = 10000 # Q libre de perdidas
rg = 1/y11.real # Resistencias del generador
r11 = 1/y11.real # resistencia de entrada
gm = abs(y21) # gm del transistor
r22 = 1/y22.real # resistencia de salida
rl = 1/y22.real # Resistencia de carga
rext = rg/2 # resistencia externa para el calculo del inductor
L1 = (1/Q1 - 1/Qo)*rext/wo # Calculo del inductor
C1 = 1/(wo**2 * L1) # Capacitor de sintonia
rp1 = Qo * wo * L1 # Resistencia de perdida
rti = Q1*wo*L1 # resistencia total en el nodo de entrada (incluye sintonizado)
rto = r22*rl/(r22 + rl) # resistencia total en el nodo de salida (no tiene sintonizado)
Av = gm * rto # Ganancia de tension
G = Av**2 * r11/rl # Ganancia de potencia
print('Ganancia de potenica: {:1.2e} V'.format(G) )
Beq1 = (np.pi/2)*(fo/Q1) # Ancho de banda equivalente del sintonizado
print('Ancho de banda equivalente: {:1.2e} Hz '.format(Beq1) )
# Calculo de la fuentes de corriente de ruido
iib = (4*kb*T/rti)**(1/2) ## Corriente de ruido dadas las resistencias en la entrada
Ni = iib**2* Beq1 *r11 # N Potencia de ruido de entrada
print('Potencia de ruido de entrada Ni: {:1.2e} W'.format(Ni))
iei = (F - 1)**(1/2) * iib ## Fuente de corriente de ruido en exceso en la entrada
# Si la fuente se encuetra en el nodo de salida
#ieo = ((F - 1)*G*rti/rto)**(1/2)*ii
inoise = (iib**2 + iei**2)**(1/2) # Corriente total en el nodo de entrada
print('Valor cuadratico medio de la corriente sobre el resistor de entrada: {:1.2e} V'.format(inoise) )
No = G * (inoise**2 * Beq1 * r11)
print('Potencia de ruido sobre el resistor de salida: {:1.2e} W'.format(No))
F = No/(G*Ni)
print('F : {:1.2e} '.format(F))
NF = 10 * np.log10(F)
print('NF : {:1.2e} '.format(NF))
Ganancia de potenica: 2.25e+03 V
Ancho de banda equivalente: 3.93e+06 Hz
Potencia de ruido de entrada Ni: 1.31e-13 W
Valor cuadratico medio de la corriente sobre el resistor de entrada: 7.26e-12 V
Potencia de ruido sobre el resistor de salida: 4.66e-10 W
F : 1.58e+00
NF : 2.00e+00
[7]:
## Parametros de LTspice
# para usar en LTspice. Presionar s y pegar en el cuadro de dialogo.
# Los valores de los componentes se asignan entre llaves.
## Para las simulaciones con LTspice
gei = iei/1e-12
print('.param L1 = {:1.3e}'.format(L1))
print('.param C1 = {:1.3e}'.format(C1))
print('.param rp1 = {:1.3e}'.format(rp1))
print('.param rg = {:1.3e}'.format(rg))
print('.param r11 = {:1.3e}'.format(r11))
print('.param gm = {:1.3e}'.format(gm))
print('.param r22 = {:1.3e}'.format(r22))
print('.param rl = {:1.3e}'.format(rl))
print('.param gei = {:1.3e}'.format(gei))
.param L1 = 1.981e-08
.param C1 = 1.278e-10
.param rp1 = 1.245e+05
.param rg = 1.000e+03
.param r11 = 1.000e+03
.param gm = 3.000e-02
.param r22 = 1.000e+04
.param rl = 1.000e+04
.param gei = 4.411e+00
Medición con LTspice¶
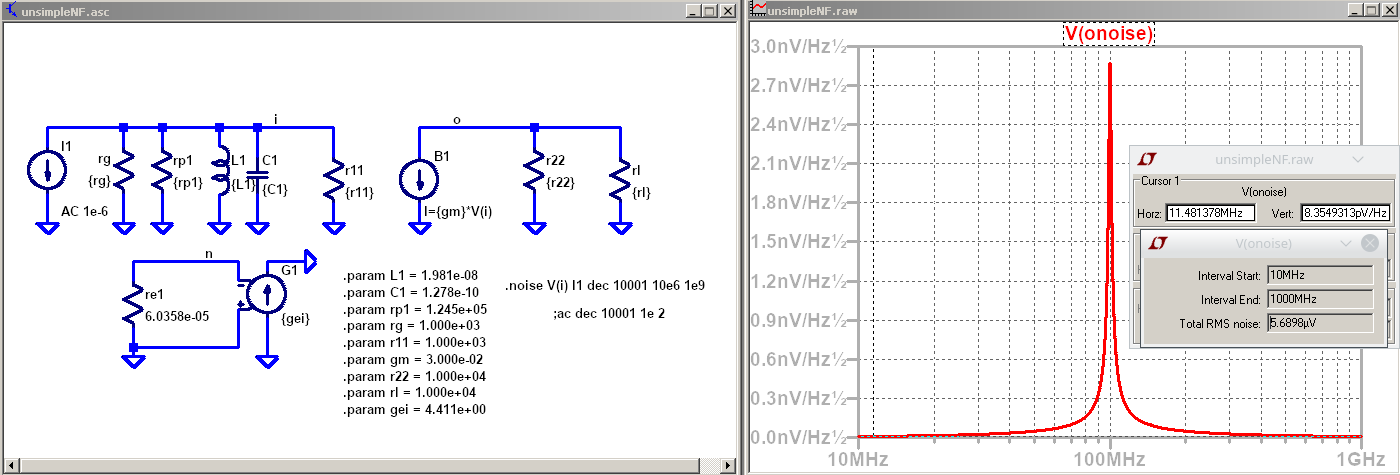
Valor cuadratico medio de la tensión en el nodo de entrada: \(5.5858e-6 V\)
Potencia de ruido sobre el resistor \(r11\):
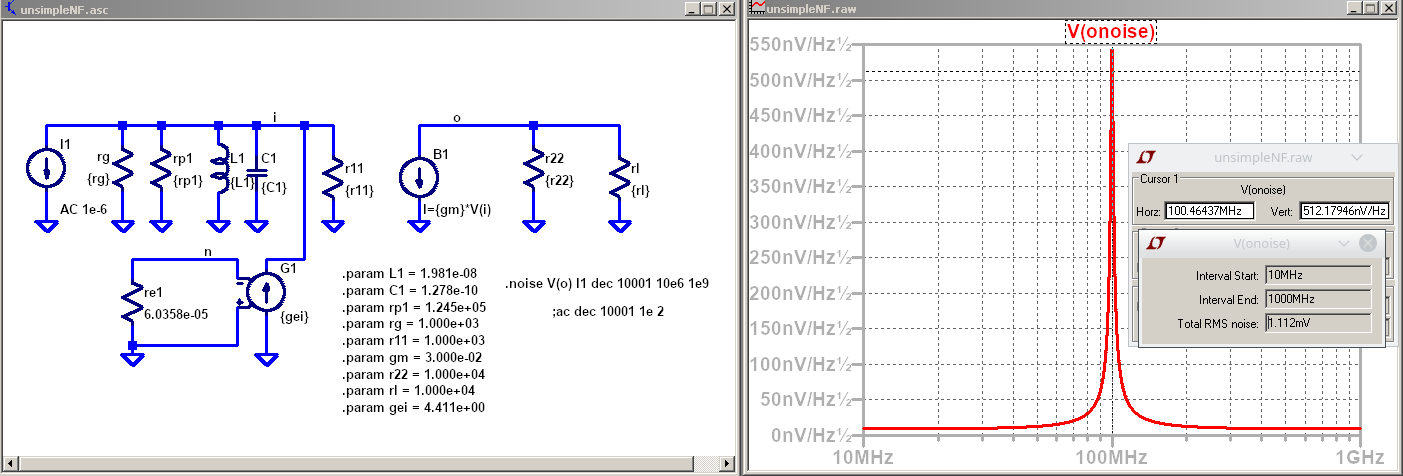
Valor cuadratico medio de la tensión en el nodo de entrada: \(1.11e-3 V\)
Potencia de ruido sobre el resistor \(rl\):
Ejemplo Dos Simples Sintonizados empleando transistor con factor de ruido \(F = 2\).¶
Calcular el ancho de banda equivalente de un amplificador simple sintonizado que tiene dos sintonizados. Calcular para máxima transferencia de energía.
Datos: \(f_o = 100 MHz\)
\(Q_{c1} = 40\) \(Q_{c2} = 40\)
\(Q_o = inf\)
Transistor:
\(y11 = 1.0\times 10^{-3}S\),
\(y12 = 0.0S\),
\(y21 = 30.0\times 10^{-3}S\),
\(y22 = 0.1\times 10^{-3}S\).
[8]:
## Ejemplo con calculo en Python
# simple sintonizado de 100MHz
# Frecuencia de operación
fo = 100e6
wo= 2*np.pi*fo
kb = constants.value('Boltzmann constant')
# Temperatura en Kelvin
T = 300
# Parametros del transistor 100 MHz
y11 = 1.0e-3
y12 = 0.0
y21 = 30.0e-3
y22 = 0.1e-3
# Cifra de ruido del transistor
NF = 2 # dB
F = 10**(NF/10) # Factor de ruido del transistor
Q1 = 40 # Q cargado del sintonizado
Q2 = 40 # Q cargado del sintonizado
Qo = 10000 # Q libre de perdidas
rg = 1/y11.real # Resistencias del generador
r11 = 1/y11.real # resistencia de entrada
gm = abs(y21) # gm del transistor
r22 = 1/y22.real # resistencia de salida
rl = 1/y22.real # Resistencia de carga
## Entrada
rext = rg/2 # resistencia externa para el calculo del inductor
L1 = (1/Q1 - 1/Qo)*rext/wo # Calculo del inductor
C1 = 1/(wo**2 * L1) # Capacitor de sintonia
rp1 = Qo * wo * L1 # Resistencia de perdida
rti = Q1*wo*L1 # resistencia total en el nodo de entrada (incluye sintonizado)
## Salida
rext = r22/2 # resistencia externa para el calculo del inductor
L2 = (1/Q2 - 1/Qo)*rext/wo # Calculo del inductor
C2 = 1/(wo**2 * L2) # Capacitor de sintonia
rp2 = Qo * wo * L2 # Resistencia de perdida
rto = Q2*wo*L2 # resistencia total en el nodo de salida (no tiene sintonizado)
Av = gm * rto # Ganancia de tension
G = Av**2 * r11/rl # Ganancia de potencia
print('Ganancia de potenica: {:1.2e} V'.format(G) )
# Ancho de banda equivalente para las fuentes de ruido en la entrada del sintonizado
Beq1 = (np.pi/2)*(fo/Q1)
print('Ancho de banda equivalente de la entrada: {:1.2e} Hz '.format(Beq1) )
# Ancho de banda equivalente para las fuentes de ruido en la salida del sintonizado
Beq2 = (np.pi/2)*(fo/Q2)
print('Ancho de banda equivalente de la salida: {:1.2e} Hz '.format(Beq2) )
# Ancho de banda equivalente para las fuentes de ruido de la entrada del sintonizado
Beq1o = (np.pi/4)*(fo/Q1)
print('Ancho de banda equivalente: {:1.2e} Hz '.format(Beq1o) )
# Calculo de la fuentes de corriente de ruido
iib = (4*kb*T/rti)**(1/2) ## Corriente de ruido dadas las resistencias en la entrada
Ni = iib**2* Beq1o *r11 # N Potencia de ruido de entrada
print('Potencia de ruido de entrada Ni: {:1.2e} W'.format(Ni))
iei = (F - 1)**(1/2) * iib ## Fuente de corriente de ruido en exceso en la entrada
# Si la fuente se encuetra en el nodo de salida
ieo = ((F - 1)*G*rti/rto)**(1/2)*iib
inoise = (iib**2 + iei**2)**(1/2) # Corriente total en el nodo de entrada
print('Valor cuadratico medio de la corriente sobre el resistor de entrada: {:1.2e} A'.format(inoise) )
No = G * (inoise**2 * Beq1o * r11)
print('Potencia de ruido sobre el resistor de salida: {:1.2e} W'.format(No))
F = No/(G*Ni)
print('F : {:1.2e} '.format(F))
NF = 10 * np.log10(F)
print('NF : {:1.2e} '.format(NF))
Ganancia de potenica: 2.23e+03 V
Ancho de banda equivalente de la entrada: 3.93e+06 Hz
Ancho de banda equivalente de la salida: 3.93e+06 Hz
Ancho de banda equivalente: 1.96e+06 Hz
Potencia de ruido de entrada Ni: 6.53e-14 W
Valor cuadratico medio de la corriente sobre el resistor de entrada: 7.26e-12 A
Potencia de ruido sobre el resistor de salida: 2.31e-10 W
F : 1.58e+00
NF : 2.00e+00
[9]:
## Parametros de LTspice
# para usar en LTspice. Presionar s y pegar en el cuadro de dialogo.
# Los valores de los componentes se asignan entre llaves.
## Para las simulaciones con LTspice
gei = iei/1e-12
geo = ieo/1e-12
print('.param rg = {:1.3e}'.format(rg))
print('.param L1 = {:1.3e}'.format(L1))
print('.param C1 = {:1.3e}'.format(C1))
print('.param rp1 = {:1.3e}'.format(rp1))
print('.param gei = {:1.3e}'.format(gei))
print('.param geo = {:1.3e}'.format(geo))
print('.param r11 = {:1.3e}'.format(r11))
print('.param gm = {:1.3e}'.format(gm))
print('.param r22 = {:1.3e}'.format(r22))
print('.param L2 = {:1.3e}'.format(L2))
print('.param C2 = {:1.3e}'.format(C2))
print('.param rp2 = {:1.3e}'.format(rp2))
print('.param rl = {:1.3e}'.format(rl))
.param rg = 1.000e+03
.param L1 = 1.981e-08
.param C1 = 1.278e-10
.param rp1 = 1.245e+05
.param gei = 4.411e+00
.param geo = 6.590e+01
.param r11 = 1.000e+03
.param gm = 3.000e-02
.param r22 = 1.000e+04
.param L2 = 1.981e-07
.param C2 = 1.278e-11
.param rp2 = 1.245e+06
.param rl = 1.000e+04
Medición con LTspice¶
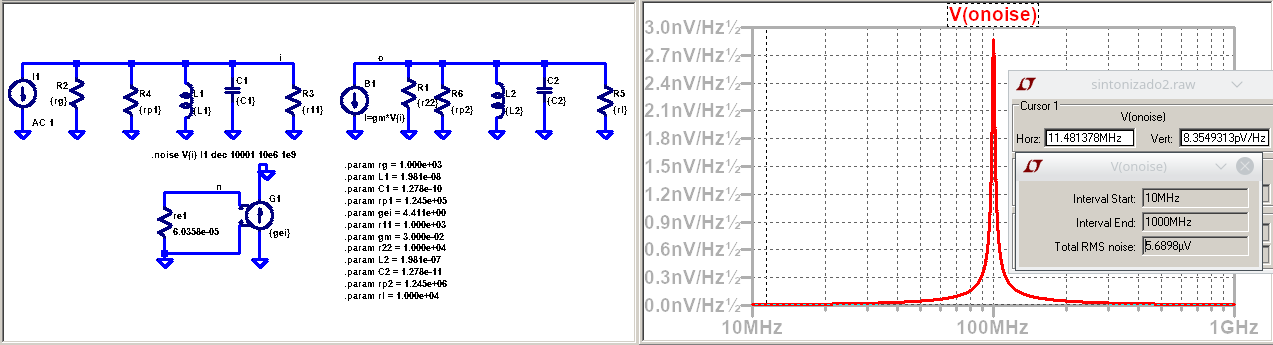
Valor cuadratico medio de la tensión en el nodo de entrada: \(5.5858e-6 V\)
Potencia de ruido sobre el resistor \(r11\):
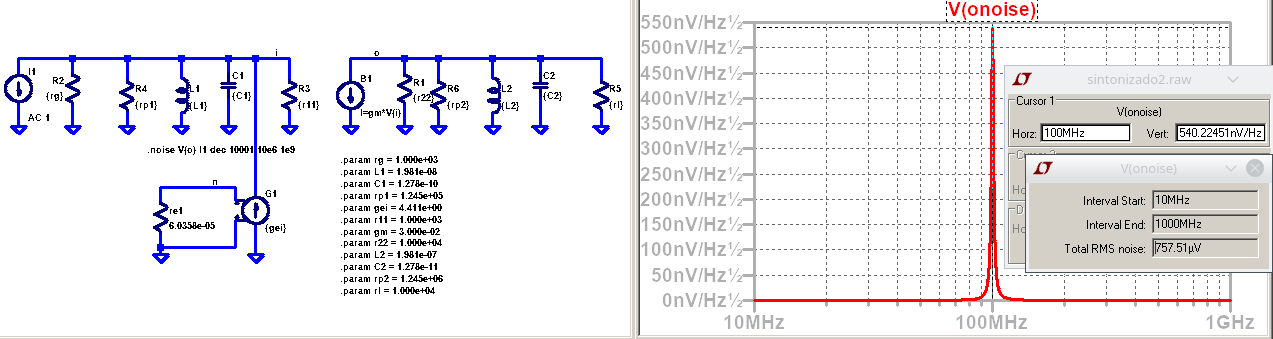
Valor cuadratico medio de la tensión en el nodo de entrada: \(757e-6 V\)
Potencia de ruido sobre el resistor \(rl\):
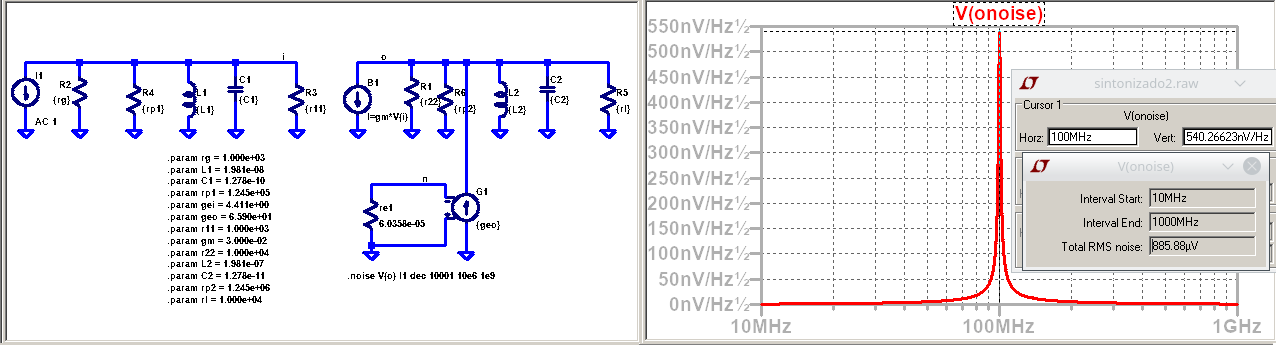
Valor cuadratico medio de la tensión en el nodo de entrada: \(885e-6 V\)
Potencia de ruido sobre el resistor \(rl\):
La diferencia entre los dos metodos radica en que la fuente de corriente de ruido en la entrada se filtra por dos sintonizados, lo que da un ancho de banda equivalente de ruido de \(\frac{\pi}{4}\), en cambio, al estar en la salida, el ancho de banda equivalente es de \(\frac{\pi}{2}\).
Ancho de banda de ruido equivalente¶
Se define como ancho de banda equivalente de ruido, al ancho de banda que debería tener un dispositivo ideal para producir en la salida la misma potencia de ruido.
La potencia de ruido a la salida del dispositivo puede calcularse integrando la densidad espectral de potencia de ruido a la salida \(N_{noise}*|H(f)|^2\) para todas las frecuencias, donde \(|H(f)|^2\) es la ganancia de potencia del dispisitivo en función de la frecuencia (puede ser un amplificador, un filtro o un mezclador). Esta potencia tiene que coincidir con la potencia a la salida de un filtro ideal de ancho de banda \(B_{eq}\) y ganancia igual a la ganancia en frecuencia central \(f_{c}\).
Esto demuestra que el ancho de banda se calcula de la siguiente forma:
Ruido en un receptor heterodino¶
La figura muestra un receptor heteronido de doble conversión.
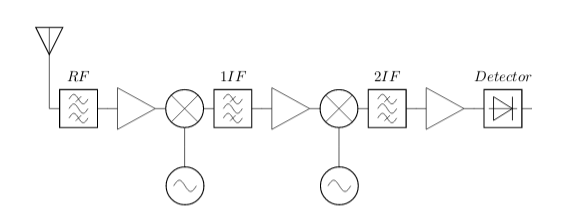
El factor de ruido del receptor se puede calcular como:
Podemos aplicar la formula de Frizz, si los anchos de banda de ruido se reducen en las sucesivas etapas.
Dado que la incidencia del factor de ruido es inversamente proporcial a las ganancias anteriores, para la mayoria de los casos prácticos, las primeras etapas son las que definen el ruido del sistema.
Con respecto al ancho de banda de ruido equivalente, podemos analizar los anchos de banda de ruido de cada etapa para ver como inciden en el ancho de banda total del sistema.
En este caso, por ejemplo, si la etapa de RF esta sintoniza en \(100 MHz\), su ancho de banda probablemente sea de algunos \(MHz\), la etapa de primera de frecuencia intermedia tiene una frecuencia de \(10.7 MHz\) con un ancho de banda de banda de cientos de \(KHz\) y por último, la etapa de segunda frecuencia intermedia esta sintonizada a \(455 KHz\) con un ancho de banda de decenas de \(KHz\). En este sistema, la cifra de ruido se define por las primeras etapas (RF y 1FI) y el ancho de banda equivalente de ruido esta definido principalmente por la etapa de segunda FI.
Tres simples sintonizados sincrónicos:¶
Donde: \(\chi^2=\frac{2 Q}{f_{o}} \cdot (f-f_{o})\), entonces \(df= \frac{f_{o}}{2Q}d\chi\).
El ancho de banda equivalente se calcula de esta forma
El ancho de banda equivalente es el ancho de banda de 3dB por \(\pi/2\)
Butterwoth de tercer orden¶
La transferencia normalizada de un Butterwoth de orden \(n\) puede expresarse como:
donde:
Esta transferencia corresponde a un filtro pasabajo, por lo tanto para el cálculo del ancho de banda equivalante podemos usar esta ecuación teniendo en cuenta que corresponde a la mitad del ancho de banda.
Entonces: